éférencer les membres directs de sa famille est chose aisée : on les connaît, ou on les a connu. Et puis, à force de rechercher dans les états civils, les archives, les sites de bourses d'échange sur Internet, on accumule une masse d'informations qui devient rapidement difficile à gérer. En effet, amasser des patronymes que l'on n'a pas connu, et dont personne de son entourage n'a finalement jamais entendu parler, nous pousse nécessairement à les classer. Reste à savoir comment! Pas par noms : le classement deviendrait (très) vite ingérable en ce sens que l'on double le nombre de patronymes à chaque génération. Ni par époque, car l'écart entre deux générations n'est pas forcément le même dans deux familles distinctes. Ni enfin par siècle, pour les mêmes raisons que précédemment. Alors comment ?

Utiliser les outils qui existent déjà! 

________________

Le tableau d'ascendance utilise une numérotation élaborée en 1590 par l'historien allemand Michel Eytzinger⁽¹⁾. En 1676, le généalogiste espagnol Jérôme de Sosa⁽²⁾ en fera usage et c'est finalement Stéphane Kekule Von Stradonitz⁽³⁾ qui lui donnera ses lettres de noblesse. Ainsi, bien que devant se nommer Numérotation d'Eytzinger, l'usage l'a baptisée Sosa-Stradonitz, plus communément appelée Sosa.

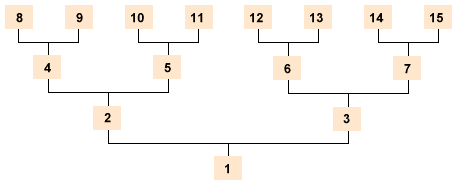
Cette numérotation présente deux avantages :

• Elle permet de repérer immédiatement les ancêtres en fonction leur sexe. En effet, les hommes portent un numéro pair et les femmes sont identifiées à l'aide d'un numéro impair ;

• Elle fait apparaître les personnages de l'implexe, c'est à dire le rapport entre le nombre théorique d'ancêtres et le nombre réel, puisque dans le cas de mariages consanguins, un ancêtre peut figurer sous deux numéros. Ce point sera soulevé un peu plus loin.

Comment ça marche ?

Un père est identifié au moyen d'un nombre égal au double de celui de son fils (ou de sa fille). Il est également égal à la moitié de celui de son propre père. Exemple : le numéro 4 a pour fils le numéro 2 (2 x 2) et pour père le numéro 8 (8 / 2).

De même, une mère est repérée grâce à un nombre égal à la somme du double de celui de son fils (ou de sa fille) et de 1. Il est par ailleurs égal à la moitié de celui de son père. Quant au rattachement au numéro de sa mère, il est égal à la différence de la moitié de celle-ci et de 1. Exemple : le numéro 7 est la mère du 3 ((2 x 3) + 1) et est la fille du 14 (14 / 2) et du 15 ((15 - 1) / 2).

Un peu de calcul!

Les matheux auront tout de suite remarqué que chaque génération débute par une puissance entière de 2, ce qui est tout à fait normal, vu qu'à chaque génération, le nombre d'individus est doublé. Ceci appelle une autre réflexion : en supposant que l'intervalle inter génésique, c'est à dire l'écart entre deux générations, soit d'environ 25 ou 30 ans, le nombre théorique d'ancêtres d'une personne née en 1999 serait d'environ 70 000 000 000 individus en 732 (Charles Martel, souvenez-vous...). Or, la population mondiale actuelle ne frise que les 10% de ce nombre. Hors de question de faire prévaloir guerres et maladies, parce que même en vertu de ces événements, si nous sommes là, c'est que nos ancêtres ont procréé!

D'où une seconde théorie, plus proche des réalités : la consanguinité. En effet, c'est bien en vertu de mariages entre parents - tout éloignés qu'ils puissent être - que la valeur théorique d'ancêtres excède de loin la valeur réelle. Ainsi, en 1663, Marie De Parenty et Marc Regnault d'Ausque s'uniront sans peut-être jamais savoir que 131 ans plus tôt sont décédés leurs arrières arrières grands parents communs : Pierre Coze et Péronne Germain. Donc au lieu d'avoir 30 trisaïeux, il n'en n'ont que 28! En second lieu, Pierre et Péronne se trouvent chacun repérés par deux numéros : un par la filiation de Marie Parenty en vertu du calcul décris ci-dessus et un second par celle de Marc Régnault.

(1) : Thesaurus prinicipum hac aetate in Europa viventium, quo progenitores eorum ... simul ac frates et sonores inde ab origine reconduntur ... usque ad annum ... 

(2) : Noticia de la gran casa de los marqueses de Villafranca.

(3) : Ahnentafel-atlas.